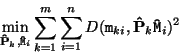Refining structure and motion

Once the structure and motion has been obtained for the whole sequence, it is recommended to refine it through a global minimization step. A maximum likelihood estimation can be obtained through bundle adjustment [21,179]. The goal is to find the projection matrices 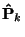${\bf\hat{P}}_k$ and the 3D points 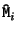${\tt\hat{M}}_i$ for which the mean squared distances between the observed image points 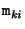${\tt m}_{ki}$ and the reprojected image points 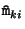${\tt\hat{m}}_{ki}$ is minimized. 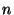For $m$ views and $n$ points the following criterion should be minimized:

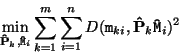$$\min_{{\bf\hat{P}}_k,{\tt\hat{M}}_i} \sum_{k=1}^{m} \sum_{i=1}^{n} D({\tt m}_{ki},{\bf\hat{P}}_k{\tt\hat{M}}_i)^2$$ (E12)

where 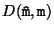$D({\tt\hat{m}},{\tt m})$ is the Euclidean image distance. If the image error is zero-mean Gaussian then bundle adjustment is the Maximum Likelihood Estimator. Although it can be expressed very simply, this minimization problem is huge. For a typical sequence of 20 views and 2000 points, a minimization problem in more than 6000 variables has to be solved. A straight-forward computation is obviously not feasible. However, the special structure of the problem can be exploited to solve the problem much more efficiently. Before going more into detail on efficiently solving the bundle adjustment, the Levenberg-Marquardt minimization is presented. Based one this an efficient method for bundle adjustment will be proposed in Section 5.4.2.