Generalized Complex Sinusoids

We have defined sinusoids and extended the definition to include complex sinusoids. We now extend one more step by allowing for exponential amplitude envelopes:

$$y(t) \isdef {\cal A}e^{st}$$

where ${\cal A}$ and $s$ are complex, and further defined as

$$\begin{eqnarray*} {\cal A}&=& Ae^{j\phi} \\ s &=& \sigma + j\omega \end{eqnarray*}$$

When $\sigma=0$, we obtain

$$y(t) \isdef {\cal A}e^{j\omega t} = A e^{j\phi} e^{j\omega t} = A e^{j(\omega t + \phi)}$$

which is the complex sinusoid at amplitude 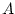$A$, frequency $\omega$, and phase $\phi$.

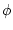More generally, we have

$$\begin{eqnarray*} y(t) &\isdef & {\cal A}e^{st} \\ &\isdef & A e^{j\phi} e^{(\... ... t} \left[\cos(\omega t + \phi) + j\sin(\omega t + \phi)\right]. \end{eqnarray*}$$

Defining $\tau = -1/\sigma$, we see that the generalized complex sinusoid is just the complex sinusoid we had before with an exponential envelope:

$$\begin{eqnarray*} \mbox{re}\left\{y(t)\right\} &=& A e^{- t/\tau} \cos(\omega t ... ...{im}\left\{y(t)\right\} &=& A e^{- t/\tau} \sin(\omega t + \phi) \end{eqnarray*}$$