 Circular Motion
Circular Motion
 Audio Decay Time (T60)
Audio Decay Time (T60)
 Sinusoids and Exponentials
Contents
Global Contents
Sinusoids and Exponentials
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
Recall Euler's Identity,
Multiplying this equation by  and setting
and setting
 , where
, where  is time in seconds,
is time in seconds,  is radian frequency, and
is radian frequency, and 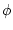 is a phase offset, we obtain what we call the complex sinusoid:
Thus, a complex sinusoid consists of an ``in-phase'' component for its
real part, and a ``phase-quadrature'' component for its imaginary
part. Since
is a phase offset, we obtain what we call the complex sinusoid:
Thus, a complex sinusoid consists of an ``in-phase'' component for its
real part, and a ``phase-quadrature'' component for its imaginary
part. Since
 , we have
That is, the complex sinusoid has a constant modulus (i.e.,
a constant complex magnitude). (The symbol
``
, we have
That is, the complex sinusoid has a constant modulus (i.e.,
a constant complex magnitude). (The symbol
`` '' means ``identically equal to,'' i.e., for all
'' means ``identically equal to,'' i.e., for all  .) The
instantaneous phase of the complex sinusoid is
The derivative of the instantaneous phase of the complex sinusoid
gives its instantaneous frequency
.) The
instantaneous phase of the complex sinusoid is
The derivative of the instantaneous phase of the complex sinusoid
gives its instantaneous frequency
Subsections
 Circular Motion
Circular Motion
 Audio Decay Time (T60)
Audio Decay Time (T60)
 Sinusoids and Exponentials
Contents
Global Contents
Sinusoids and Exponentials
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)

