 Matrix Multiplication
Matrix Multiplication
 Round-Off Error Variance
Round-Off Error Variance
 MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT)
Contents
Global Contents
MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT)
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
Matrices
A matrix is defined as a rectangular array of numbers, e.g.,
which is a  (``two by two'') matrix. A general matrix may
be
(``two by two'') matrix. A general matrix may
be  , where
, where  is the number of rows,
and
is the number of rows,
and  is the number of columns of the matrix.
For example, the general
is the number of columns of the matrix.
For example, the general  matrix is
Either square brackets or large parentheses may be used to
delimit the matrix. The
matrix is
Either square brackets or large parentheses may be used to
delimit the matrix. The
 th elementD.1 of a
matrix
th elementD.1 of a
matrix 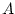 may be denoted by
may be denoted by ![$ A[i,j]$](img1520.png) or
or  . The rows and
columns of matrices are normally numbered from
. The rows and
columns of matrices are normally numbered from 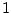 instead of from
0; thus,
instead of from
0; thus,
 and
and
 . When
. When  , the
matrix is said to be square.
, the
matrix is said to be square.
The transpose of a real matrix
 is denoted by
is denoted by
 and is defined by
and is defined by
Note that while 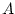 is
is  , its transpose is
, its transpose is  .
.
A complex matrix
 , is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
, is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
 and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by
and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by  and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
Example: The transpose of the general  matrix is
matrix is
while the conjugate transpose of the general  matrix is
matrix is
A column vector, e.g.,
is the special case of an  matrix, and a row vector, e.g.,
(as we have been using) is a
matrix, and a row vector, e.g.,
(as we have been using) is a  matrix. In contexts where
matrices are being used (only this section for this book), it is best to
define all vectors as column vectors and to indicate row vectors
using the transpose notation, as was done in the equation above.
matrix. In contexts where
matrices are being used (only this section for this book), it is best to
define all vectors as column vectors and to indicate row vectors
using the transpose notation, as was done in the equation above.
Subsections
 Matrix Multiplication
Matrix Multiplication
 Round-Off Error Variance
Round-Off Error Variance
 MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT)
Contents
Global Contents
MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT)
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)
![$\displaystyle A = \left[\begin{array}{cc} a & b \\ [2pt] c & d \end{array}\right]
$](img1514.png)
![$\displaystyle A = \left[\begin{array}{cc} a & b \\ [2pt] c & d \end{array}\right]
$](img1514.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right]
$](img1518.png)
![]() is denoted by
is denoted by
![]() and is defined by
and is defined by
![]() , is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
, is simply a
matrix containing complex numbers. The
transpose of a complex matrix is normally defined to
include conjugation. The conjugating transpose operation is called the
Hermitian transpose. To avoid confusion, in this tutorial,
![]() and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by
and the word ``transpose'' will always denote transposition
without conjugation, while conjugating transposition will be
denoted by ![]() and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
and be called the ``Hermitian transpose'' or the
``conjugate transpose.'' Thus,
![]() matrix is
matrix is
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right...
...\tiny T}}
=
\left[\begin{array}{ccc} a & c & e \\ b & d & f \end{array}\right]
$](img1532.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right...
...\overline{e }\\
\overline{b} & \overline{d} & \overline{f }\end{array}\right]
$](img1533.png)
![$\displaystyle \underline{x}= \left[\begin{array}{c} x_0 \\ [2pt] x_1 \end{array}\right]
$](img1534.png)