- ...
numbers.1.1
- Physicists and mathematicians use
 instead of
instead of
 to denote
to denote  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
unknowns.2.1
- ``Linear'' in this context means that the unknowns
are multiplied only by constants--they may not be multiplied by each
other or raised to any power other than
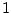 (e.g., not squared or cubed
or raised to the
(e.g., not squared or cubed
or raised to the  power). Linear systems of
power). Linear systems of  equations in
equations in  unknowns are very easy to solve compared to nonlinear systems
of
unknowns are very easy to solve compared to nonlinear systems
of  equations in
equations in  unknowns. For example, Matlab and Octave can
easily handle them. You learn all about this in a course on
Linear Algebra which is highly recommended for anyone
interested in getting involved with signal processing. Linear algebra
also teaches you all about matrices, which are introduced only
briefly in Appendix D.
unknowns. For example, Matlab and Octave can
easily handle them. You learn all about this in a course on
Linear Algebra which is highly recommended for anyone
interested in getting involved with signal processing. Linear algebra
also teaches you all about matrices, which are introduced only
briefly in Appendix D.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
numbers2.2
- (multiplication, addition, division, distributivity
of multiplication over addition, commutativity of multiplication and
addition)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...field.2.3
- See, e.g.,
Eric Weisstein's World of Mathematics
(http://mathworld.wolfram.com/) for definitions of any
unfamiliar mathematical terms such as a field (which is described,
for example, at the easily guessed URL
http://mathworld.wolfram.com/Field.html).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tool.2.4
- Proofs for the
fundamental theorem of algebra have a long history involving many of
the great names in classical mathematics. The first known rigorous
proof was by Gauss based on earlier efforts by Euler and Lagrange.
(Gauss also introduced the term ``complex number.'') An alternate
proof was given by Argand based on the ideas of d'Alembert. For a
summary of the history, see http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Fund_theorem_of_algebra.html
(the first Google search result for ``fundamental theorem of
algebra'' in July of 2002).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as3.1
- This was computed via N[Sqrt[2],60] in Mathematica.
Symbolic mathematics programs, such as Mathematica,
Maple (offered as a Matlab extension),
maxima (a GNU descendant of the original Macsyma), or
Yacas (another free, open-source program with similar goals
as Mathematica), are handy tools for cranking out any number
of digits in irrational numbers such as
 . In
Yacas (as of Version 1.0.55), the syntax is
. In
Yacas (as of Version 1.0.55), the syntax is
Precision(60)
N(Sqrt(2))
Of course, symbolic math programs can do much more than this, such as
carrying out algebraic manipulations on polynomials and solving
systems of symbolic equations in closed form.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3.2
- Logarithms are reviewed in Appendix B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
number3.3
- A number is said to be
transcendental if it is not a
root of any polynomial with integer coefficients, i.e., it is not an
algebraic number of any degree. (Irrational numbers are
algebraic numbers of degree 1.) See http://mathworld.wolfram.com/TranscendentalNumber.html
for further discussion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by3.4
- In Mathematica, the first 50 digits of
 may be computed by
the expression N[E,50] (``evaluate numerically the
reserved-constant E to 50 decimal places''). In
Yacas, one types the following:
may be computed by
the expression N[E,50] (``evaluate numerically the
reserved-constant E to 50 decimal places''). In
Yacas, one types the following:
Precision(50)
N(Exp(1))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
unity.3.5
- Sometimes we see
 , which is
the complex conjugate of the definition we have used here.
, which is
the complex conjugate of the definition we have used here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (LTI4.1
- A system
 is said to be
linear if for any two input signals
is said to be
linear if for any two input signals  and
and  , we have
, we have
![$ S[x_1(t) + x_2(t)] = S[x_1(t)] + S[x_2(t)]$](img353.png) . A system is said to be
time invariant if
. A system is said to be
time invariant if
![$ S[x(t-\tau)] = y(t-\tau)$](img354.png) , where
, where
![$ y(t)\isdef
S[x(t)]$](img355.png) . This subject is developed in detail in the on-line book
[56].
. This subject is developed in detail in the on-line book
[56].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
dB4.2
- Decibels (dB) are reviewed in Appendix B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...combfilter.4.3
- Technically, Fig. 4.3 shows the
feedforward comb filter, also called the ``inverse comb
filter'' [60]. The longer names are meant to
distinguish it from the feedback comb filter, in which the
delay output is fed back around the delay line and summed with
the delay input instead of the input being fed forward around
the delay line and summed with its output. (A diagram and further
discussion, including how time-varying comb filters create a
flanging effect, can be found at
http://ccrma-www.stanford.edu/~jos/waveguide/Feedback_Comb_Filters.html.)
The frequency response of the feedforward comb filter is the inverse
of that of the feedback comb filter (one can cancel the effect of the
other), hence the name ``inverse comb filter.'' Frequency-response analysis
of digital filters is developed in the on-line book [56].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... name.4.4
- While there is no reason it should be obvious
at this point, the comb-filter gain varies in fact sinusoidally
between
 and
and  . It looks more ``comb'' like on a dB amplitude
scale, which is more appropriate for audio applications.
. It looks more ``comb'' like on a dB amplitude
scale, which is more appropriate for audio applications.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dc4.5
- ``dc'' means ``direct current'' and is an
electrical engineering term for ``frequency 0''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dB.4.6
- Recall that a gain factor
 is converted to decibels (dB) by the formula
is converted to decibels (dB) by the formula
 . See §B.2 for a review.
. See §B.2 for a review.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... signal.4.7
- In complex variables, ``analytic'' just
means differentiable of all orders. Therefore, one might expect an
``analytic signal'' to be any signal which is differentiable of all
orders at any point in time, i.e., one that admits a fully valid Taylor
expansion about any point in time. However, all bandlimited
signals (being sums of finite-frequency sinusoids) are analytic in the
complex-variables sense. Therefore, the signal processing term
``analytic signal'' is used to mean a signal having ``no negative
frequencies''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... shift.4.8
- This operation is actually
used in some real-world AM and FM radio receivers (particularly in digital
radio receivers). The signal comes in centered about a high ``carrier
frequency'' (such as 101 MHz for radio station FM 101), so it looks very
much like a sinusoid at frequency 101 MHz. (The frequency modulation only
varies the carrier frequency in a relatively tiny interval about 101 MHz.
The total FM bandwidth including all the FM ``sidebands'' is about 100 kHz.
AM bands are only 10kHz wide.) By delaying the signal by 1/4 cycle, a good
approximation to the imaginary part of the analytic signal is created, and
its instantaneous amplitude and frequency are then simple to compute from
the analytic signal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,4.9
- If
 were constant, this would be
exact.
were constant, this would be
exact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...demodulation4.10
- Demodulation is the process of
recovering the modulation signal. For amplitude modulation (AM), the
modulated signal is of the form
 ,
where
,
where  is the ``carrier frequency'',
is the ``carrier frequency'',
![$ A(t)=[1+\mu x(t)]\geq 0$](img454.png) is the amplitude envelope (modulation),
is the amplitude envelope (modulation),  is the modulation
signal we wish to recover (the audio signal being broadcast in the case of
AM radio), and
is the modulation
signal we wish to recover (the audio signal being broadcast in the case of
AM radio), and  is the modulation index for AM.
is the modulation index for AM.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kHz,4.11
- or very close to that--I once
saw Sony device using a sampling rate of
 Hz.
Hz.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 4.12
4.12
- The notation
 denotes a single sample
of the signal
denotes a single sample
of the signal  at sample
at sample  , while the notation
, while the notation  or
simply
or
simply  denotes the entire signal for all time.
denotes the entire signal for all time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... projection4.13
- The coefficient of projection of a signal
 onto another signal
onto another signal  can be thought of as a measure of how much of
can be thought of as a measure of how much of
 is present in
is present in  . We will consider this topic in some detail
later on.
. We will consider this topic in some detail
later on.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5.1
5.1
- We'll use an underline to emphasize the vector
interpretation, but there is no difference between
 and
and
 . For
purposes of this book, a signal is the same thing as a
vector.
. For
purposes of this book, a signal is the same thing as a
vector.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hear,5.2
- Actually,
two-sample signals with variable amplitude and spacing between the
samples provide very interesting tests of pitch perception, especially
when the samples have opposite sign [45].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... units.5.3
- The energy of a
pressure wave is the integral over time of the squared pressure
divided by the wave impedance the wave is traveling in. The energy of
a velocity wave is the integral over time of the squared
velocity times the wave impedance. In audio work, a signal
 is
typically a list of pressure samples derived from a microphone
signal, or it might be samples of force from a piezoelectric
transducer, velocity from a magnetic guitar pickup, and so on.
In all of these cases, the total physical energy associated with the
signal is proportional to the sum of squared signal samples.
Physical connections in signal processing are explored more fully in
[55].
is
typically a list of pressure samples derived from a microphone
signal, or it might be samples of force from a piezoelectric
transducer, velocity from a magnetic guitar pickup, and so on.
In all of these cases, the total physical energy associated with the
signal is proportional to the sum of squared signal samples.
Physical connections in signal processing are explored more fully in
[55].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
removed:5.4
- For reasons beyond the scope of this book, when the
sample mean
 is estimated as the average value of the same
is estimated as the average value of the same  samples used to compute the sample variance
samples used to compute the sample variance
 , the sum
should be divided by
, the sum
should be divided by  rather than
rather than  to avoid a bias
[28].
to avoid a bias
[28].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vector.5.5
- You might wonder why the norm of
 is
not written as
is
not written as
 . There would be no problem with this
since
. There would be no problem with this
since
 is otherwise undefined.
However, the historically adopted notation is
instead
is otherwise undefined.
However, the historically adopted notation is
instead
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...).6.1
- The Matlab code for generating this figure is given
in §I.4.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... unity.6.2
- The notations
 ,
,  , and
, and  are
common in the digital signal processing literature. Sometimes
are
common in the digital signal processing literature. Sometimes  is defined with a negative exponent, i.e.,
is defined with a negative exponent, i.e.,
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
by6.3
- The notation
 means the whole signal
means the whole signal
 ,
,
 . This is also written as simply
. This is also written as simply  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filter.6.4
- More precisely,
 is a length
is a length  finite-impulse-response (FIR) digital
filter. See §8.3 for related discussion.
finite-impulse-response (FIR) digital
filter. See §8.3 for related discussion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... computed,6.5
- We call
this the
aliased sinc function
to distinguish it from the sinc function
sinc
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dftfilterb6.6
- The Matlab code for this figure is
given in §I.4.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
spectra7.1
- A spectrum is mathematically identical to a signal, since
both are just sequences of
 complex numbers. However, for clarity, we
generally use ``signal'' when the sequence index is considered a time
index, and ``spectrum'' when the index is associated with successive
frequency samples.
complex numbers. However, for clarity, we
generally use ``signal'' when the sequence index is considered a time
index, and ``spectrum'' when the index is associated with successive
frequency samples.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
convolution).7.2
- To simulate acyclic convolution, as is
appropriate for the simulation of sampled continuous-time systems,
sufficient zero padding is used so that nonzero samples do not ``wrap
around'' as a result of the shifting of
 in the definition of
convolution. Zero padding is discussed later in this
chapter (§7.2.6).
in the definition of
convolution. Zero padding is discussed later in this
chapter (§7.2.6).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....7.3
- Matched filtering is briefly
discussed in §8.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... domain.7.4
- Similarly, zero padding in the
frequency domain gives what we call ``periodic interpolation'' in the
time domain which is exact in the DFT case only for periodic signals
having a time-domain period equal to the DFT length. (See
§7.4.13.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... times.7.5
- You might wonder why we need this
since all indexing in
 is defined modulo
is defined modulo  already. The answer
is that
already. The answer
is that
 formally expresses a mapping from the space
formally expresses a mapping from the space
 of length
of length  signals to the space
signals to the space  of length
of length  signals.
signals.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....7.6
- The function
 is also considered odd,
ignoring the singularity at
is also considered odd,
ignoring the singularity at  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transform,7.7
- The discrete cosine
transform (DCT) used often in applications is actually defined
somewhat differently (see §H.3.1), but the basic principles are
the same
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transform7.8
- The FFT is just a fast implementation of
the DFT. See Appendix H for details and pointers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FFT.7.9
- These results
were obtained using the program Octave running on a Linux PC
with a 2.8GHz Pentium CPU, and Matlab running on a Windows PC
with an 800MHz Athlon CPU.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...table:ffttable.7.10
- These results were obtained using
Matlab running on a Windows PC with an 800MHz Athlon CPU.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dual7.11
- The dual of a Fourier operation
is obtained by interchanging time and frequency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequency7.12
- The
folding frequency is defined as half the sampling rate
 .
It may also be called the Nyquist limit. The Nyquist
rate, on the other hand, means the sampling rate, not half
the sampling rate.
.
It may also be called the Nyquist limit. The Nyquist
rate, on the other hand, means the sampling rate, not half
the sampling rate.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FIR7.13
- FIR stands for
``finite-impulse-response.'' Digital filtering concepts and
terminology are introduced in §8.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FFT8.1
- Recall that the FFT is just a high-speed
implementation of the DFT, discussed further in Appendix H.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
system8.2
- Linearity and time invariance are introduced in
the second book of this series [56].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...estimator8.3
- In signal processing, a ``hat'' often denotes an estimated quantity.
Thus,
 is an estimate of
is an estimate of  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... value8.4
- For present purposes, the expected value
 may be found by averaging an infinite number of sample
cross-correlations
may be found by averaging an infinite number of sample
cross-correlations
 computed using different segments of
computed using different segments of
 and
and  . Both
. Both  and
and  must be infinitely long, of course, and
all stationary processes are infinitely long. Otherwise, their
statistics could not be time invariant.
must be infinitely long, of course, and
all stationary processes are infinitely long. Otherwise, their
statistics could not be time invariant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8.5
- See
Eq. (7.1) for a definition of
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
density''.8.6
- To clarify, we are using the word ``sample'' with
two different meanings. In addition to the usual meaning wherein a
continuous time or frequency axis is made discrete, a statistical
``sample'' refers to a set of observations from some presumed random
process. Estimated statistics based on such a statistical sample are
then called ``sample statistics'', such as the sample mean, sample
variance, and so on.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8.7
- Since phase information is discarded
(
 ),
the zero-padding can go before or after
),
the zero-padding can go before or after  ,
or both, without affecting the results.
,
or both, without affecting the results.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kernel;8.8
- By the convolution theorem dual, windowing
in the time domain is convolution (smoothing) in the frequency domain
(§7.4.6). Since a triangle is the convolution of a
rectangle with itself, its transform is
sinc
 in the
continuous-time case (cf. Appendix G). In the discrete-time
case, it is proportional to
in the
continuous-time case (cf. Appendix G). In the discrete-time
case, it is proportional to
 sinc
sinc .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pulse,A.1
- Thanks to Miller
Puckette for suggesting this example.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energy).A.2
- One joke along these lines, due, I'm
told, to Professor Bracewell at Stanford, is that ``since the
telephone is bandlimited to 3kHz, and since bandlimited signals cannot
be time limited, it follows that one cannot hang up the telephone''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... belB.1
- The ``bel'' is named after Alexander
Graham Bell, the inventor of the telephone.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... intensity,B.2
-
Intensity is
physically power per unit area. Bels may also be defined in
terms of energy, or power which is energy per unit time.
Since sound is always measured over some
area by a microphone diaphragm, its physical power is conventionally
normalized by area, giving intensity. Similarly, the force applied
by sound to a microphone diaphragm is normalized by area to give
pressure (force per unit area).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 B.3
B.3
- The bar was originally defined as
$10^-6$ atmospheres, but now it is defined to be exactly
1 $dyne/cm^2$.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
distortion'').B.4
- Companders (compressor-expanders) essentially
``turn down'' the signal gain when it is ``loud'' and ``turn up'' the
gain when it is ``quiet''. As long as the input-output curve is
monotonic (such as a log characteristic), the dynamic-range
compression can be undone (expanded).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 0.C.1
- Computers use bits, as opposed to the more
familiar decimal digits, because they are more convenient to implement
in digital hardware. For example, the decimal numbers 0, 1, 2,
3, 4, 5 become, in binary format, 0, 1, 10, 11, 100, 101. Each
bit position in binary notation corresponds to a power of 2,
e.g.,
 ; while each
digit position in decimal notation corresponds to a power of
10, e.g.,
; while each
digit position in decimal notation corresponds to a power of
10, e.g.,
 . The term
``digit'' comes from the same word meaning ``finger.'' Since
we have ten fingers (digits), the term ``digit'' technically should be
associated only with decimal notation, but in practice it is used for
others as well. Other popular number systems in computers include
octal which is base 8 (rarely seen any more, but still
specifiable in any C/C++ program by using a leading zero, e.g.,
. The term
``digit'' comes from the same word meaning ``finger.'' Since
we have ten fingers (digits), the term ``digit'' technically should be
associated only with decimal notation, but in practice it is used for
others as well. Other popular number systems in computers include
octal which is base 8 (rarely seen any more, but still
specifiable in any C/C++ program by using a leading zero, e.g.,
 decimal = 111,101,101
binary), and hexadecimal (or simply ``hex'') which is
base 16 and which employs the letters A through F to yield 16 digits
(specifiable in C/C++ by starting the number with ``0x'', e.g., 0x1ED
=
decimal = 111,101,101
binary), and hexadecimal (or simply ``hex'') which is
base 16 and which employs the letters A through F to yield 16 digits
(specifiable in C/C++ by starting the number with ``0x'', e.g., 0x1ED
=
 decimal =
1,1110,1101 binary). Note, however, that the representation within
the computer is still always binary; octal and hex are simply
convenient groupings of bits into sets of three bits (octal)
or four bits (hex).
decimal =
1,1110,1101 binary). Note, however, that the representation within
the computer is still always binary; octal and hex are simply
convenient groupings of bits into sets of three bits (octal)
or four bits (hex).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... processors.C.2
- This information is subject to change
without notice. Check your local compiler documentation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
feedbackC.3
- Normally, quantization error is computed as
 , where
, where  is the signal being quantized, and
is the signal being quantized, and
![$ {\hat x}(n) = Q[x(n)]$](img1460.png) is the quantized value, obtained by rounding to the
nearest representable amplitude. Filtered error feedback uses instead
the formula
is the quantized value, obtained by rounding to the
nearest representable amplitude. Filtered error feedback uses instead
the formula
![$ {\hat x}(n) = Q[x(n)+{\cal L}\{e(n-1)\}]$](img1461.png) , where
, where
 denotes a filtering operation which ``shapes'' the quantization noise
spectrum. An excellent article on the use of round-off error feedback
in audio digital filters is
[14].
denotes a filtering operation which ``shapes'' the quantization noise
spectrum. An excellent article on the use of round-off error feedback
in audio digital filters is
[14].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... most-significant).C.4
- Remember that byte
addresses in a big endian word start at the big end of the word, while
in a little endian architecture, they start at the little end of the
word.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
``endianness'':C.5
- Thanks to Bill Schottstaedt for help with this table.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,C.6
- The notation
 denotes a half-open interval which includes
denotes a half-open interval which includes  but not
but not  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....C.7
- Another term commonly heard for ``significand''
is ``mantissa.'' However, this use of the term ``mantissa'' is not the same
as its previous definition as the fractional part of a logarithm. We will
therefore use only the term ``significand'' to avoid confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bias.C.8
- By choosing
the bias equal to half the numerical dynamic range of
 (thus effectively
inverting the sign bit of the exponent), it becomes easier to compare two
floating-point numbers in hardware: the entire floating-point word can be
treated by the hardware as one giant integer for numerical comparison
purposes. This works because negative exponents correspond to
floating-point numbers less than 1 in magnitude, while. positive exponents
correspond to floating-point numbers greater than 1 in magnitude.
(thus effectively
inverting the sign bit of the exponent), it becomes easier to compare two
floating-point numbers in hardware: the entire floating-point word can be
treated by the hardware as one giant integer for numerical comparison
purposes. This works because negative exponents correspond to
floating-point numbers less than 1 in magnitude, while. positive exponents
correspond to floating-point numbers greater than 1 in magnitude.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...CODEC|textbfC.9
- CODEC is an acronym for ``COder/DECoder''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elementD.1
- We are now using
 as an integer counter,
not as
as an integer counter,
not as  . This is standard notational practice.
. This is standard notational practice.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
argument.D.2
- Alternatively, it can be extended to the complex case by
writing
![$ A^{\ast }B \isdef [\ldots<b_j,a^{\ast }_i>\ldots]$](img1547.png) , so that
, so that
 includes a conjugation of the elements of
includes a conjugation of the elements of 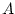 . This
difficulty arises from the fact that matrix multiplication is really
defined without consideration of conjugation or transposition at all,
making it unwieldy to express in terms of inner products in the complex
case, even though that is perhaps the most fundamental interpretation
of a matrix multiply.
. This
difficulty arises from the fact that matrix multiplication is really
defined without consideration of conjugation or transposition at all,
making it unwieldy to express in terms of inner products in the complex
case, even though that is perhaps the most fundamental interpretation
of a matrix multiply.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variable,E.1
- Most of this appendix uses
normalized frequency, i.e., the sampling rate equals
 sample per second.
sample per second.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
seconds,E.2
- A signal
 is said to be periodic with
period
is said to be periodic with
period  if
if
 for all
for all
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... isE.3
- To obtain precisely this
result, it is necessary to define
 via a limiting pulse
converging to time 0 from the right of time 0, as we have done
in Eq. (E.3).
via a limiting pulse
converging to time 0 from the right of time 0, as we have done
in Eq. (E.3).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... principle|textbf.F.1
- The Heisenberg uncertainty principle in quantum physics
applies to any dual properties of a particle. For example, the
position and velocity of an electron are oft-cited as such duals. An
electron is described, in quantum mechanics, by a probability wave
packet. Therefore, the position of an electron in space can be
defined as the midpoint of the amplitude envelope of its wave
function; its velocity, on the other hand, is determined by the
frequency of the wave packet. To accurately measure the
frequency, the packet must be very long in space, to provide many
cycles of oscillation under the envelope. But this means the location
in space is relatively uncertain. In more precise mathematical terms,
the probability wave function for velocity is proportional to the
spatial Fourier transform of the probability wave for position. I.e.,
they are exact Fourier duals. The Heisenberg Uncertainty Principle is
therefore a Fourier property of fundamental particles described by
waves [16].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filter.F.2
- An allpass filter has unity gain and
arbitrary delay at each frequency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
principle.G.1
- An early derivation of the sampling theorem is
often cited as a 1928 paper by Harold Nyquist, and Claude Shannon is
credited with reviving interest in the sampling theorem after World
War II when computers became public. As a result, the sampling
theorem is often called ``Nyquist's theorem,'' ``Shannon's sampling
theorem,'' or the like.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
positionG.2
- More typically, each sample represents the
instantaneous velocity of the speaker. Here's why: Most
microphones are transducers from acoustic pressure to
electrical voltage, and analog-to-digital converters (ADCs)
produce numerical samples which are proportional to voltage. Thus,
digital samples are normally proportional to acoustic pressure
deviation (force per unit area on the microphone, with ambient air
pressure subtracted out). When digital samples are converted to
analog form by digital-to-analog conversion (DAC), each sample is
converted to an electrical voltage which then drives a loudspeaker (in
audio applications). Typical loudspeakers use a ``voice-coil'' to
convert applied voltage to electromotive force on the speaker which
applies pressure on the air via the speaker cone. Since the acoustic
impedance of air is a real number, wave pressure is directly
proportional wave velocity. Since the speaker must move in
contact with the air during wave generation, we may conclude that
digital signal samples correspond most closely to the velocity
of the speaker, not its position. The situation is further
complicated somewhat by the fact that typical speakers do not
themselves have a real driving-point impedance.
However, for an ``ideal'' microphone and speaker, we should get
samples proportional to speaker velocity and hence to air pressure.
Well below resonance, the real radiation impedance of the pushed air
should dominate, as long as the excursion does not exceed the linear
interval of cone displacement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....G.3
- Mathematically,
 can be allowed to be nonzero over points
can be allowed to be nonzero over points
 provided that the set of all such points have measure zero in
the sense of Lebesgue integration. However, such distinctions do not
arise for practical signals which are always finite in extent and
which therefore have continuous Fourier transforms. This is why we
specialize the sampling theorem to the case of continuous-spectrum
signals.
provided that the set of all such points have measure zero in
the sense of Lebesgue integration. However, such distinctions do not
arise for practical signals which are always finite in extent and
which therefore have continuous Fourier transforms. This is why we
specialize the sampling theorem to the case of continuous-spectrum
signals.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
compositeH.1
- In this context, ``highly composite'' means ``a
product of many prime factors.'' For example, the number
 is highly composite since it is a power of 2. The
number
is highly composite since it is a power of 2. The
number
 is also composite, but it
requires prime factors other than 2. Prime numbers
is also composite, but it
requires prime factors other than 2. Prime numbers
 are not composite at all.
are not composite at all.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fftsw.H.2
- Additionally,
an excellent ``home page'' on the fast Fourier transform is located
at http://ourworld.compuserve.com/homepages/steve_kifowit/fft.htm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gain.H.3
- This result is well known in the field of
image processing. The DCT performs almost as well as the optimal
Karhunen-Loève Transform (KLT) when analyzing certain Gaussian
stochastic processes as the transform size goes to infinity. (In the
KLT, the basis functions are taken to be the eigenvectors of the
autocorrelation matrix of the input signal block. As a result, the
transform coefficients are decorrelated in the KLT, leading to
maximum energy concentration and optimal coding gain.) However, the
DFT provides a similar degree of optimality for large block sizes
 .
For practical spectral analysis and processing of audio signals, there
is typically no reason to prefer the DCT over the DFT.
.
For practical spectral analysis and processing of audio signals, there
is typically no reason to prefer the DCT over the DFT.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.