 Solving Linear Equations Using Matrices
Solving Linear Equations Using Matrices
 Matrices
Matrices
 Matrices
Contents
Global Contents
Matrices
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
Let
 be a general
be a general  matrix and let
matrix and let  denote a general
denote a general
 matrix. Denote the matrix product by
matrix. Denote the matrix product by
 or
or
 . Then matrix multiplication is carried out by computing the inner product of every row of
. Then matrix multiplication is carried out by computing the inner product of every row of
 with every column of
with every column of  . Let the
. Let the
 th row of
th row of
 be denoted by
be denoted by
 ,
,
 , and the
, and the
 th column of
th column of  by
by
 ,
,
 . Then the matrix product
. Then the matrix product
 is defined as
is defined as
This definition can be extended to complex matrices by using a
definition of inner product which does not conjugate its second
argument.D.2
Examples:
An  matrix
matrix 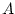 can be multiplied on the right by an
can be multiplied on the right by an
 matrix, where
matrix, where  is any positive integer. An
is any positive integer. An  matrix
matrix 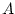 can be multiplied on the left by a
can be multiplied on the left by a  matrix, where
matrix, where  is any positive integer. Thus, the number of columns in
the matrix on the left must equal the number of rows in the matrix on the
right.
is any positive integer. Thus, the number of columns in
the matrix on the left must equal the number of rows in the matrix on the
right.
Matrix multiplication is non-commutative, in general. That is,
normally  even when both products are defined (such as when the
matrices are square.)
even when both products are defined (such as when the
matrices are square.)
The transpose of a matrix product is the product of the
transposes in reverse order:
The identity matrix is denoted by  and is defined as
and is defined as
Identity matrices are always square. The  identity
matrix
identity
matrix  , sometimes denoted as
, sometimes denoted as  , satisfies
, satisfies
 for every
for every
 matrix
matrix 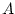 . Similarly,
. Similarly,
 , for every
, for every  matrix
matrix 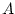 .
.
As a special case, a matrix
 times a vector
times a vector
 produces a new vector
produces a new vector
 which consists of the inner product of every row of
which consists of the inner product of every row of
 with
with

A matrix
 times a vector
times a vector
 defines a linear transformation
of
defines a linear transformation
of
 . In fact, every linear function of a vector
. In fact, every linear function of a vector
 can be
expressed as a matrix multiply. In particular, every linear
filtering operation can be expressed as a matrix multiply applied to the
input signal. As a special case, every linear, time-invariant (LTI)
filtering operation can be expressed as a matrix multiply in which the
matrix is
Toeplitz,
i.e.,
can be
expressed as a matrix multiply. In particular, every linear
filtering operation can be expressed as a matrix multiply applied to the
input signal. As a special case, every linear, time-invariant (LTI)
filtering operation can be expressed as a matrix multiply in which the
matrix is
Toeplitz,
i.e.,
![$ A^{\hbox{\tiny T}}[i,j] = A^{\hbox{\tiny T}}[i-j]$](img1561.png) (constant along
diagonals).
(constant along
diagonals).
As a further special case, a row vector on the left may be multiplied by a
column vector on the right to form a single inner product:
Use of the ``Hermitian transpose'' notation `` ''
(defined in §6.10) allows the the above result to hold also
for complex vectors. We may now rewrite the general matrix
multiply as
''
(defined in §6.10) allows the the above result to hold also
for complex vectors. We may now rewrite the general matrix
multiply as
 Solving Linear Equations Using Matrices
Solving Linear Equations Using Matrices
 Matrices
Matrices
 Matrices
Contents
Global Contents
Matrices
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)
![]() be a general
be a general ![]() matrix and let
matrix and let ![]() denote a general
denote a general
![]() matrix. Denote the matrix product by
matrix. Denote the matrix product by
![]() or
or
![]() . Then matrix multiplication is carried out by computing the inner product of every row of
. Then matrix multiplication is carried out by computing the inner product of every row of
![]() with every column of
with every column of ![]() . Let the
. Let the
![]() th row of
th row of
![]() be denoted by
be denoted by
![]() ,
,
![]() , and the
, and the
![]() th column of
th column of ![]() by
by
![]() ,
,
![]() . Then the matrix product
. Then the matrix product
![]() is defined as
is defined as
![$\displaystyle C = A^{\hbox{\tiny T}}B = \left[\begin{array}{cccc}
<\underline{...
...\cdots & <\underline{a}^{\hbox{\tiny T}}_M,\underline{b}_N>
\end{array}\right]
$](img1546.png)
![$\displaystyle \left[\begin{array}{cc} a & b \\ c & d \\ e & f \end{array}\right...
...gamma & c\beta+d\delta \\
e\alpha+f\gamma & e\beta+f\delta
\end{array}\right]
$](img1548.png)
![$\displaystyle \left[\begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{ar...
...ma a + \delta b & \gamma c + \delta d & \gamma e + \delta f
\end{array}\right]
$](img1549.png)
![$\displaystyle \left[\begin{array}{c} \alpha \\ \beta \end{array}\right]
\cdot
\...
...pha a & \alpha b & \alpha c \\
\beta a & \beta b & \beta c
\end{array}\right]
$](img1550.png)
![$\displaystyle \left[\begin{array}{ccc} a & b & c \end{array}\right]
\cdot
\left...
...} \alpha \\ \beta \\ \gamma \end{array}\right]
= a \alpha + b \beta + c \gamma
$](img1551.png)
![]() matrix
matrix ![]() can be multiplied on the right by an
can be multiplied on the right by an
![]() matrix, where
matrix, where ![]() is any positive integer. An
is any positive integer. An ![]() matrix
matrix ![]() can be multiplied on the left by a
can be multiplied on the left by a ![]() matrix, where
matrix, where ![]() is any positive integer. Thus, the number of columns in
the matrix on the left must equal the number of rows in the matrix on the
right.
is any positive integer. Thus, the number of columns in
the matrix on the left must equal the number of rows in the matrix on the
right.
![]() even when both products are defined (such as when the
matrices are square.)
even when both products are defined (such as when the
matrices are square.)
![]() and is defined as
and is defined as
![$\displaystyle I \isdef \left[\begin{array}{ccccc}
1 & 0 & 0 & \cdots & 0 \\
0...
...dots & \vdots & \cdots & \vdots \\
0 & 0 & 0 & \cdots & 1
\end{array}\right]
$](img1554.png)
![]() times a vector
times a vector
![]() produces a new vector
produces a new vector
![]() which consists of the inner product of every row of
which consists of the inner product of every row of
![]() with
with
![]()
![$\displaystyle A^{\hbox{\tiny T}}\underline{x}= \left[\begin{array}{c}
<\underl...
...\vdots \\
<\underline{a}^{\hbox{\tiny T}}_M,\underline{x}>
\end{array}\right]
$](img1560.png)
![$\displaystyle C = A^{\hbox{\tiny T}}B = \left[\begin{array}{cccc}
\underline{a...
...& \cdots & \underline{a}^{\hbox{\tiny T}}_M \underline{b}_N
\end{array}\right]
$](img1564.png)