 DFT Problems
DFT Problems
 The Length 2 DFT
The Length 2 DFT
 The DFT Derived
Contents
Global Contents
The DFT Derived
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
Matrix Formulation of the DFT
The DFT can be formulated as a complex matrix multiply, as we show in
this section. (This section can be omitted without affecting what
follows.) For basic definitions regarding matrices, see
Appendix D.
The DFT consists of inner products of the input signal
 with sampled complex sinusoidal sections
with sampled complex sinusoidal sections
 :
:
By collecting the DFT output samples into a column vector, we have
or
where  denotes the DFT matrix
denotes the DFT matrix
![$ S_N[k,n]\isdef W_N^{-kn} \isdef
e^{-j2\pi k n/N}$](img878.png) , or,
, or,
We see that the  th row of the DFT matrix is the
th row of the DFT matrix is the  th DFT sinusoid.
Since the matrix is symmetric,
th DFT sinusoid.
Since the matrix is symmetric,
 (where
transposition does not include conjugation), we observe that
the
(where
transposition does not include conjugation), we observe that
the  th column of
th column of  is also the
is also the  th DFT sinusoid.
Computation of the DFT matrix in Matlab is illustrated in
§I.4.3.
th DFT sinusoid.
Computation of the DFT matrix in Matlab is illustrated in
§I.4.3.
The inverse DFT matrix is simply
 . That is,
we can perform the inverse DFT operation as
. That is,
we can perform the inverse DFT operation as
where
 denotes the Hermitian
transpose of the complex matrix
denotes the Hermitian
transpose of the complex matrix 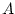 (transposition and complex
conjugation). Since
(transposition and complex
conjugation). Since
 , the above implies
The above equation succinctly implies that the columns of
, the above implies
The above equation succinctly implies that the columns of  are
orthogonal, which, of course, we already knew.
are
orthogonal, which, of course, we already knew.
The normalized DFT matrix is given by
and the corresponding
normalized inverse DFT matrix is simply
 , so that we have
This implies that the columns of
, so that we have
This implies that the columns of  are orthonormal. Such a
complex matrix is said to be unitary.
are orthonormal. Such a
complex matrix is said to be unitary.
When a real matrix 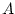 satisfies
satisfies
 , then
, then 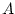 is said to be
orthogonal.
``Unitary'' is the generalization of ``orthogonal'' to
complex matrices.
is said to be
orthogonal.
``Unitary'' is the generalization of ``orthogonal'' to
complex matrices.
 DFT Problems
DFT Problems
 The Length 2 DFT
The Length 2 DFT
 The DFT Derived
Contents
Global Contents
The DFT Derived
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)
![]() with sampled complex sinusoidal sections
with sampled complex sinusoidal sections
![]() :
:

![$\displaystyle \left[\begin{array}{c}
X(\omega_0) \\
X(\omega_1) \\
X(\omega_...
...gin{array}{c}
x(0) \\
x(1) \\
x(2) \\
\vdots \\
x(N-1)
\end{array}\right]
$](img875.png)
![\begin{eqnarray*}
S_N &\isdef &
\left[\begin{array}{cccc}
s_0(0) & s_0(1) & \cd...
...2(N-1)/N} & \cdots & e^{-j 2\pi (N-1)(N-1)/N}
\end{array}\right]
\end{eqnarray*}](img879.png)
![]() th row of the DFT matrix is the
th row of the DFT matrix is the ![]() th DFT sinusoid.
Since the matrix is symmetric,
th DFT sinusoid.
Since the matrix is symmetric,
![]() (where
transposition does not include conjugation), we observe that
the
(where
transposition does not include conjugation), we observe that
the ![]() th column of
th column of ![]() is also the
is also the ![]() th DFT sinusoid.
Computation of the DFT matrix in Matlab is illustrated in
§I.4.3.
th DFT sinusoid.
Computation of the DFT matrix in Matlab is illustrated in
§I.4.3.
![]() . That is,
we can perform the inverse DFT operation as
. That is,
we can perform the inverse DFT operation as


![]() satisfies
satisfies
![]() , then
, then ![]() is said to be
orthogonal.
``Unitary'' is the generalization of ``orthogonal'' to
complex matrices.
is said to be
orthogonal.
``Unitary'' is the generalization of ``orthogonal'' to
complex matrices.