Relation between the fundamental matrix and image homographies

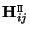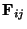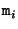There also exists an important relationship between the homographies ${\bf H}_{ij}^{\tt\Pi}$ and the fundamental matrices ${\bf F}_{ij}$. Let ${\tt m}_i$ be a point in image 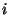$i$. Then 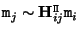${\tt m}_j\sim {\bf H}^{\tt\Pi}_{ij} {\tt m}_i$ is the corresponding point for the plane 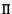${\tt\Pi }$ in image 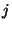$j$. Therefore, 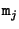${\tt m}_j$ is located on the corresponding epipolar line; and,

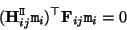$$({\bf H}^{\tt\Pi}_{ij}{\tt m}_i)^\top{\bf F}_{ij} {\tt m}_i = 0$$ (C27)

should be verified. Moreover, equation (3.27) holds for every image point 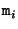${\tt m}_i$. Since the fundamental matrix maps points to corresponding epipolar lines, 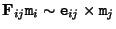${\bf F}_{ij} {\tt m}_i \sim {\tt e}_{ij} \times {\tt m}_j$ and equation (3.27) is equivalent to ${\tt m}_j^\top [{\tt e}_{ij}]_\times {\bf H}^{\tt\Pi}_{ij} {\tt m}_i=0$. 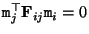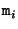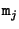Comparing this equation with ${\tt m}_j^\top {\bf F}_{ij} {\tt m}_i=0$, and using that these equations must hold for all image points ${\tt m}_i$ and ${\tt m}_j$ lying on corresponding epipolar lines, it follows that:

$${\bf F}_{ij} \sim [{\tt e}_{ij}]_\times {\bf H}_{ij}^{\tt\Pi} \enspace .$$ (C28)

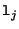Let ${\tt l}_j$ be a line in image 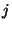$j$ and let 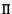${\tt\Pi }$ be the plane obtained by back-projecting 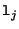${\tt l}_j$ into space. If 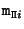${\tt m}_{{\tt\Pi}i}$ is the image of a point of this plane projected in image 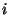$i$, then the corresponding point in image 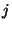$j$ must be located on the corresponding epipolar line (i.e. 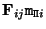${\bf F}_{ij}{\tt m}_{{\tt\Pi}i}$). Since this point is also located on the line 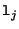${\tt l}_j$ it can be uniquely determined as the intersection of both (if these lines are not coinciding): 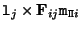${\tt l}_j \times {\bf F}_{ij} {\tt m}_{{\tt\Pi}i}$. Therefore, the homography 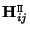${\bf H}^{\tt\Pi}_{i j }$ is given by $[{\tt l}_j]_\times {\bf F}_{ij}$. 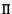Note that, since the image of the plane ${\tt\Pi }$ is a line in image 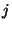$j$, this homography is not of full rank. An obvious choice to avoid coincidence of 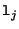${\tt l}_j$ with the epipolar lines, is 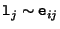${\tt l}_j \sim {\tt e}_{ij}$ since this line does certainly not contain the epipole (i.e. 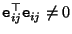${\tt e}_{ij}^\top {\tt e}_{ij} \neq 0$). Consequently,

$$[{\tt e}_{ij}]_\times {\bf F}_{ij}$$ (C29)

corresponds to the homography of a plane. By combining this result with equations (3.16) and (3.17) one can conclude that it is always possible to write the projection matrices for two views as

$$\begin{array}{rcl} {\bf P}_1 & = & [ {\bf I}_{3 \times 3} \,... ...\tt e}_{12} {\tt\pi}^\top \, \vert \,{\tt e}_{12} ] \end{array}$$ (C30)

Note that this is an important result, since it means that a projective camera setup can be obtained from the fundamental matrix which can be computed from 7 or more matches between two views. Note also that this equation has 4 degrees of freedom (i.e. the 3 coefficients of ${\tt\pi}$ and the arbitrary relative scale between ${\bf F}_{12}$ and ${\tt e}_{12}$). Therefore, this equation can only be used to instantiate a new frame (i.e. an arbitrary projective representation of the scene) and not to obtain the projection matrices for all the views of a sequence (i.e. compute ${\bf P}_3, {\bf P}_4, \ldots$). 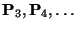How this can be done is explained in Section 5.2.